Extended version of software including the pressure dependency of solubility
Software for calculating solubility equilibrium under pressure
A program for calculating solid-liquid equilibrium in aqueous systems with the ions Na+, H+, Mg2+, Ca2+, Ba2+, Sr2+, Cl–, OH–, SO42-, HSO4–, CO32-, HCO3– , and CO2 up to high pressures is available. The program is an extended version of the program for phase equilibrium calculations offered at this site. This software for scale calculation under high pressure is meant for applications in geothermal energy production and oil field scale calculation.
Formation water is usually saturated with the minerals of the reservoir rock surrounding it. During oil production, temperature, pressure and composition of the brine might change, causing precipitation of some of these salts. This is called scale formation or scale deposition. When formation water is mixed with other brines, some salts might become supersaturated and form scale too.
The program presented here can be used for determining the risk of scale formation as a function of temperature, pressure and composition. Output from the program includes the saturation index (degree of saturation), which gives an indication of the proximity to saturation.
In geothermal energy production, sometimes the brine is diluted before it is re-injected. By doing that, the osmotic pressure of the brine can be exploited and precipitation of salts in valves, pumps and the pores at the injection site can be avoided. The amount of dilution required can be calculated with this program.
The thermodynamic model applied in the program is the Extended UNIQUAC model, using a set of model parameters based on the model parameters determined by Ada Vilafáfila Garcia and published in:
- Ada Villafáfila García, Kaj Thomsen, and Erling H. Stenby, Prediction of Mineral Scale Formation in Geothermal and Oilfield Operations using the Extended UNIQUAC Model. Part I: Sulphate Scaling Minerals, (Geothermics, 34(2005)61-97) DOI:10.1016/j.geothermics.2004.11.002 and
- Ada Villafáfila García, Kaj Thomsen, and Erling H. Stenby, Prediction of Mineral Scale Formation in Geothermal and Oilfield operations using the Extended UNIQUAC Model. Part II: Carbonate Scaling Minerals, (Geothermics 35(2006)239-284) DOI:10.1016/j.geothermics.2006.03.001
The model parameters published in these two papers were later further improved based on experimental data not available at the time of publication.
Further details on salt solution thermodynamics can be found at
and in “Electrolyte Solutions: Thermodynamics, Crystallization, Separation methods” by Kaj Thomsen which can be downloaded without cost at:
The solubility of approximately 60 different solid phases is considered and the amount of precipitate reported by the program:
NaHCO3, Na2CO3, Na2CO3·H2O, Na2CO3·7H2O, Na2CO3·10H2O, Na2CO3·3NaHCO3, Na2CO3·NaHCO3·2H2O, Na2CO3·2Na2SO4, NaCl, NaCl·2H2O, NaOH, NaOH·H2O, 2NaOH·7H2O, NaHSO4, Na2SO4, Na2SO4·10H2O, Na2SO4·CaSO4, Na2SO4·MgSO4·4H2O, 2Na2SO4·2MgSO4·5H2O, 3Na2SO4·MgSO4, MgCO3, MgCl2, MgCl2·2H2O, MgCl2·4H2O, MgCl2·6H2O, MgCl2·8H2O, MgCl2·12H2O, MgCl2·2CaCl2·6H2O, 2MgCl2·CaCl2·12H2O, Mg(OH)2, MgSO4, MgSO4·H2O, MgSO4·6H2O, MgSO4·7H2O, MgSO4·12H2O, CaCO3, CaCO3·MgCO3, CaCl2, CaCl2·H2O, CaCl2·2H2O, CaCl2·4H2O, CaCl2·6H2O, CaCl2·Ca(OH)2·H2O, Ca(OH)2, CaSO4, 2CaSO4·H2O, CaSO4·2H2O, Ba(HCO3)2, BaCO3, BaCl2, BaCl2·H2O, BaCl2·2H2O, BaCl2·Ba(OH)2·16H2O, Ba(OH)2, Ba(OH)2·H2O, Ba(OH)2·3H2O, BaSO4, SrCO3, SrCl2, SrCl2·H2O, SrCl2·2H2O, SrCl2·6H2O, Sr(OH)2, Sr(OH)2·H2O, Sr(OH)2·8H2O, SrSO4, Ice.
Sample calculations
The solubility of salts in water depends on
- Temperature
- Pressure
- The presence of other salts in the solution
- The presence of other solvents in the solution
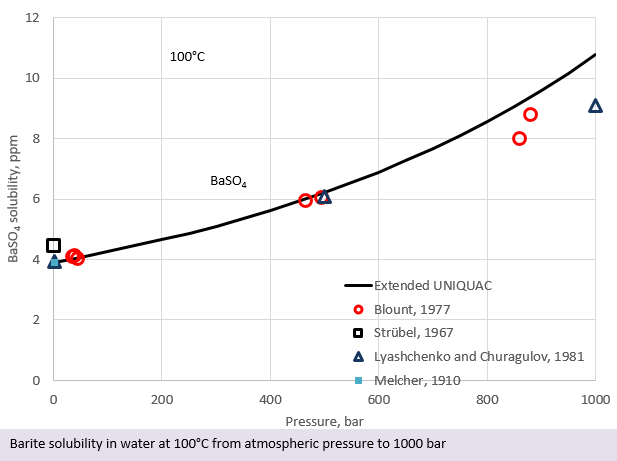
For ordinary industrial purposes, the pressure dependence of salt solubility can often be ignored. In the oil industry and in geothermal energy production, the pressure dependence on solubility can play a significant role. Many salts are most soluble at high pressure and will precipitate when the pressure is relieved. In the figure above, the solubility of barite (BaSO4) at a constant temperature of 100°C and at pressures varying from 1 bar to 1000 bar is shown. From this figure, it is seen that the solubility of barite doubles if the pressure is increased from atmospheric pressure to 1000 bar at 100°C.
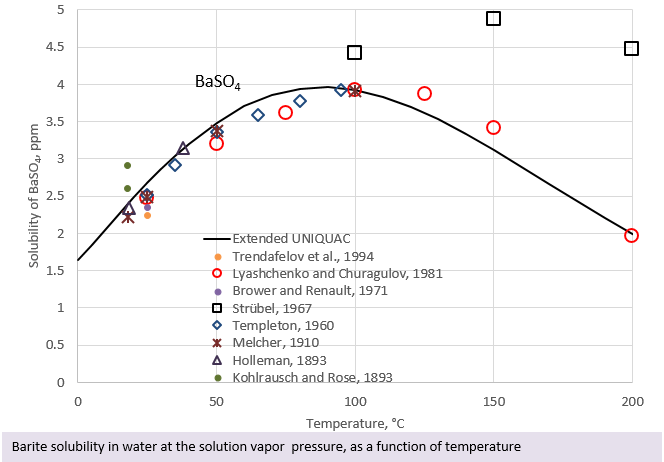
In the second figure, the solubility of barite at ambient pressure and at temperatures varying from 0 to 200°C is shown. It can be seen that the solubility of barite goes through a maximum at a temperature of approximately 90°C. This figure illustrates the conditions at low pressure. At higher pressure (at least up to 500 bar), the same phenomenon is seen, barite solubility goes through a maximum at a temperature around 90°C. If a solution is saturated with barite at 90°C it can be expected that barite will precipitate upon cooling or heating of the solution or if the pressure is lowered.
From the above figures it can be seen that the prediction of barite solubility as a function of temperature and pressure is not a trivial task. In addition, brines often contain NaCl, which also influences the solubility of barite. Software for scale calculation under high pressure is therefore helpful for predicting the risk of scaling
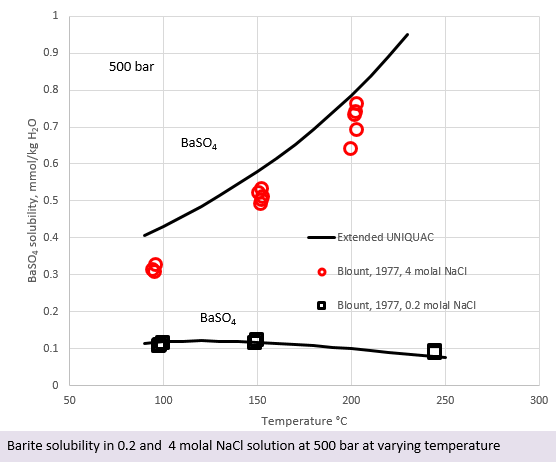
In the figure to the left, barite solubility in 0.2 molal NaCl and in 4 molal NaCl is plotted as a function of temperature. The figure contains experimental data points and lines calculated with the Extended UNIQUAC model. The data in this figure are for the solubility at 500 bar. It is interesting to see that the solubility of barite increases with temperature in the 4 molal NaCl solution, while it slightly decreases in the low NaCl concentration, as it does in water.
The increased barite solubility in concentrated NaCl solutions is a result of “salting in”. No complex formation is taking place. “Salting in” is a common phenomenon in electrolyte solutions, whereby the solubility of one salt increases due to the presence of another salt.
The phenomenon of a maximum solubility of BaSO4 is not unusual either. All sulfates seem to have a maximum solubility at some temperature. At temperatures higher than this maximm solubility temperature, the solubility decreases and usually becomes very low near the critical temperature of water. At the critical temperature of water, the relative permittivity (dielectric constant) of liquid water is very low causing the electrostatic forces between ions to increase.
The concentration unit for BaSO4 used in the figure with NaCl brines is mmol/kg water, while it is ppm on mass basis in the two figures above. The presence of NaCl in the phase diagram to the left contributes to the total mass of the solution and the ppm values would therefore not be comparable to the ppm values above.
Carbonate scaling
The solubility of carbonates is influenced by the same factors as mentioned above for barite. In addition, the solubility of carbonates is strongly dependent on the partial pressure of CO2. If the partial pressure of CO2 is reduced, the pH and the concentration of carbonate ions tend to increase, causing carbonates to precipitate. Similarly, sulfide solubility is dependent on the partial pressure of H2S.
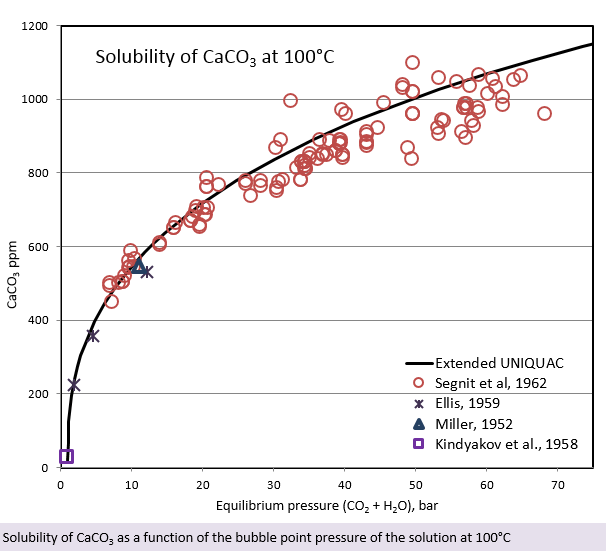
In the figure, the solubility of CaCO3 is plotted against the partial pressure of CO2 plus the partial pressure of water. While the solubility of CaCO3 is approximately 18 ppm at 100°C at atmospheric pressure, it increases rapidly in the presence of CO2. The solubility of CaCO3 at 100°C and 70 bar total pressure (partial pressure of CO2 + partial pressure of water) is 1150 ppm! Software for scale calculation under high pressure is very important for predicting such solubility development. During oil production, the CO2 pressure is eventually lowered, resulting in the evaporation of CO2 and a corresponding decrease in the solubility of calcite and other carbonates. This decrease of solubility means precipitation of carbonates.
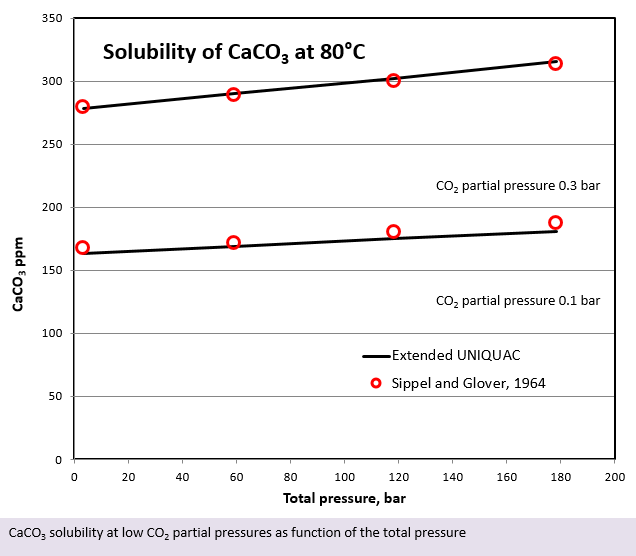
Besides the CO2 partial pressure, the solubility of CaCO3 is also influenced by the total pressure impacting the solution. This is illustrated in the last figure. The solubility of CaCO3 is apparently slightly increasing at increasing total pressure.